Forecast reconciliation

Imagine you work in a retail company and you are responsible for forecasting total sales in the following weeks. The company is spread through the country, and the forecast must be made for every city and state.

However, when the national and regional sales teams meet, your forecasts aren't consistent. "How can we sum state-level sales and find a number larger than the national one?". Which forecasts should they consider to base their decisions on?

Forecast reconciliation methods are simple and effective solutions to that problem. When you have an hierarchy of time-series that respect some linear constraints (such as the sum of state sales must be equal to national sales), you may forecast each level independently and reconciliate them.

Let's suppose our company is based on Europe and has two branches: one in France and another in Italy, and we were asked for a seven-days-ahead estimation.

The intuition

Consider this dataset containing two years of sales of a company:

The total sales in Europe is the sum of French and Italian sales, and they should follow a linear constraint defined by

Note that it can be regarded as a 2d plane in a three-dimensional space: to be considered coherent, our observations and forecasts must lie on that plane.

Applying well-known statistical forecasting methods such as ARIMA and ETS won't necessarily generate estimates that adhere to that constraint. The figure below illustrates how forecasts of an ARIMA model can diverge from it.

It seems that we can't rely on those methods. Forecasting each level independently is not enough. How can we guarantee that we'll give good quality and coherent forecasts?

Forecasting coherently

The literature provides two main approaches to forecast coherently: the single-level approach and reconciliation methods (Athanasopoulos et al., 2020).

Single-level approaches

Single-level approaches choose one level of hierarchy to produce estimates and then expand the forecasts to other levels.

The bottom-up requires forecasts for the most disaggregated levels of the hierarchy. Let $n$ be the total number of series and $m$ the number of bottom-level series. In our sales example, $n=3$ and $m=2$. The coherent forecasts are given by:

where $y_{T+h|T} \in \mathbb{R}^n$ is the h-step-ahead base forecasts for all series, $b_{T+h|T} \in \mathbb{R}^m$ our h-step-ahead forecasts for bottom-level ones. $S$ is the matrix that captures the hierarchy constraints. In the case of our sales forecasting problem, it's equal to:

and

These levels, however, are usually the most volatile and with lower signal-to-noise ratio. Another approach is the top-down, which forecasts the top-level time-series $\hat{t}_{t}$ and then disaggregate it to build forecasts for lower levels in the hierarchy:

The proportions $p \in \mathbb{R}^m$ may be estimated from historical observations (Gross & Sohl, 1990). This approach, on the other hand, is not capable of capturing particularities of the other levels in the hierarchy. Single-level approaches have the advantage of being simpler, but they don't take advantage of the information in other levels. Reconciliation methods solve this issue by using correlations of all series to get a coherent estimate.

Forecast reconciliation

Remember how our observations lay on a plane and incoherent forecasts lay outside of it in Figure 2. Let $\mathbf{s} \subset \mathbb{R}^n$ be this coherent subspace, a m-dimensional space for which the linear constraints hold. We can say that our h-step-ahead forecasts $y_{T+h|T}$ will be coherent if $y_{T+h|T} \in \mathbf{s}$. If we get our base forecasts and project them onto the coherent subspace, we'll get coherent forecasts.

The work of Panagiotelis et al., 2021 provided this geometric view of forecast reconciliation. They reframed the forecast reconciliation problem as "how should our projection matrix be so that our error metric $E$ is reduced?"$.$ If you want to ensure all your forecasts will be better after reconciliation, you may enjoy the properties of orthogonal projection. This procedure, however, considers that all errors in the hierarchy should be treated equally, which is not always the case. The forecast of total sales, for example, might be more important than sales in a specific country. Or maybe France plays a critic role in the business.

In such cases, you may go for oblique projections. They work as if the axes with less relevance were stretched before proceeding with an orthogonal projection. There's also a special kind of oblique projection that minimizes the expected error, using an estimate of the error covariance matrix Wickramasuriya et al., 2019. They called it MinT reconciliation.

Orthogonal projection

The orthogonal projection has an interesting property of being the solution in $\mathbb{s}$ closest to the base forecasts $\hat{y}_t$. In other words, it solves the optimization problem:

where $\tilde{y}_t$ is the reconciled forecast. Hereafter, we'll use tilde to represent forecasts after reconciliation, and a hat to represent our base forecasts. The projection matrix $P_s \in \mathbb{R}^{n \times n}$ can be built directly from the matrix $S$ which captures the hierarchical structure.

where $G \in \mathbb{R}^{m \times n }$ maps $\hat{y}_{T+h|T}$ to $\mathbb{R}^m$, producing new bottom-level forecasts.

We can easily reconcile our forecasts:

If one of the requirements is to change the base forecasts as least as possible, orthogonal projection is the way to go. However, it considers that all errors in the hierarchy are equally important.

Oblique projection

When you want to avoid some errors in the hierarchy more than others, oblique projection is a good choice. It can be seen as an orthogonal projection in a space with another metric $\vert\vert v \vert\vert_W = v^TWv$, where W is a positive definite matrix. In that case, the projection matrix is:

Note that $W = \mathbb{I}$ is equivalent to orthogonal projection in euclidean space. Pythagoras theorem guarantees that $\tilde{y}_{t}$ will always be closer to the true $y_{t}$ than the base forecast $\hat{y}_t$ in terms of $\vert\vert \cdot \vert\vert_{W}$:

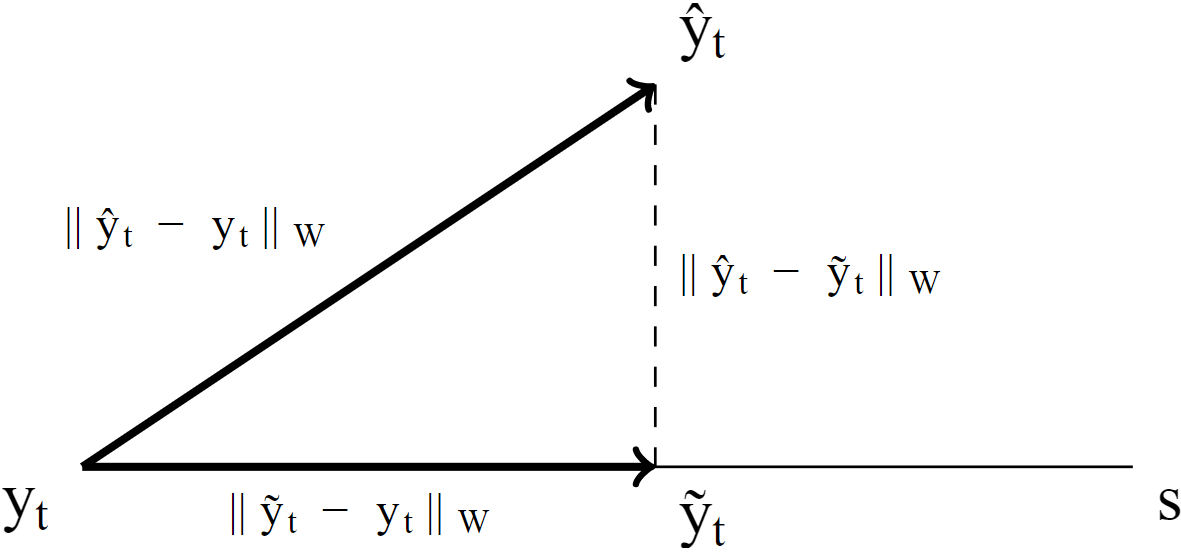
If, for example, we apply an oblique projection to our sales forecasts with $W = \begin{bmatrix} 4 & 0 & 0 \\ 0 & 4 & 0 \\ 0 & 0 & 1 \end{bmatrix}$, we obtain the following result:

MinT reconciliation

While those solutions ensure better estimates, they aren't optimal in terms of expected error. They suppose a distance metric and find the coherent forecasts that change the base forecasts as least as possible. The MinT reconciliation approach, on the other hand, minimizes the expected distance between the reconciled forecasts and the true values, even if that means changing considerably the base forecasts. The optimization problem it tries to solve is

where

where $\Sigma_h$ is the error covariance matrix of h-steps-ahead forecasts. Equation 1 says that, by minimizing the trace of the h-steps-ahead covariance matrix of $\tilde{e}_{T+h|T}$, we can reduce the expected error after reconciliation. The optimal $\tilde{y}_{T+h|T}$ can be obtained by the oblique projection of $\hat{y}_{T+h|T}$:

where

Still, we have to estimate $\Sigma_h$, which is unknown. The literature provides two choices Athanasopoulos et al., 2020:

• $\Sigma_h = \frac{1}{T}\sum\limits_{t=1}^T \hat{e}_{t+h | t}$, a naive unconstrained estimator for covariance matrix also known as sample covariance matrix. While this method is simple and works well for small hierarchies, it does not provide reliable results when the number of series grows. The reconciliation method with this estimator is called MinT(sample).

• An improved estimator of the covariance matrix proposed by Schäfer & Strimmer, 2005 and Ledoit & Wolf, 2004, which has one of funniest titles I've ever seen. The shrinkage estimator is $\Sigma^{(shrunk)}_t = \lambda \,diag(\Sigma_h) + (1 - \lambda)\Sigma_h$ and the shrinkage intensity parameter $\lambda$ can be computed from the estimated correlation matrix $r_{ij}$:

This estimator safeguards the positive-definite property of the covariance matrix, and works better when then number of observations is not considerably larger than the number of series in the hierarchy. The reconciliation method with this estimator is called MinT(shrink).

Conclusion

This post was meant to be a brief introduction to hierarchical forecasting. Some advances in reconciliation methods have been made in recent years, and we should expect more to come. The implemention of those methods is fairly simple, and the benefits are sure. The fable package in R implements them, but it should be straightforward to code from scratch in other languages. Feel free to contact me if you need some help.